In this tutorial, we will show you how, using logic and clues, you can fill in the logic grid and determine what order the given information should be in.
For this tutorial, we shall be using a 3x3x4 grid. This means there are three main squares across the top, as well as three from top to bottom. Inside each square, there is a 4 x 4 grid of smaller squares. These are the squares you will be working with to solve this puzzle. Work along with us by visiting the puzzle:
Let us first start by looking at our information. We have 4 different:
Just looking at the information, you might notice that the medication names are all ending in "pril". This is done on purpose to further confuse you while reading clues. You need to be extra careful when you have names that are similar to each other so that you do not accidentally mark the wrong name.
Now, we will look at each clue in the puzzle and show you the corresponding results on the grid table for each clue. You can follow along and by the end, you should have a basic knowledge of how to solve logic grid puzzles! So, let's begin.
The first clue we're given is:
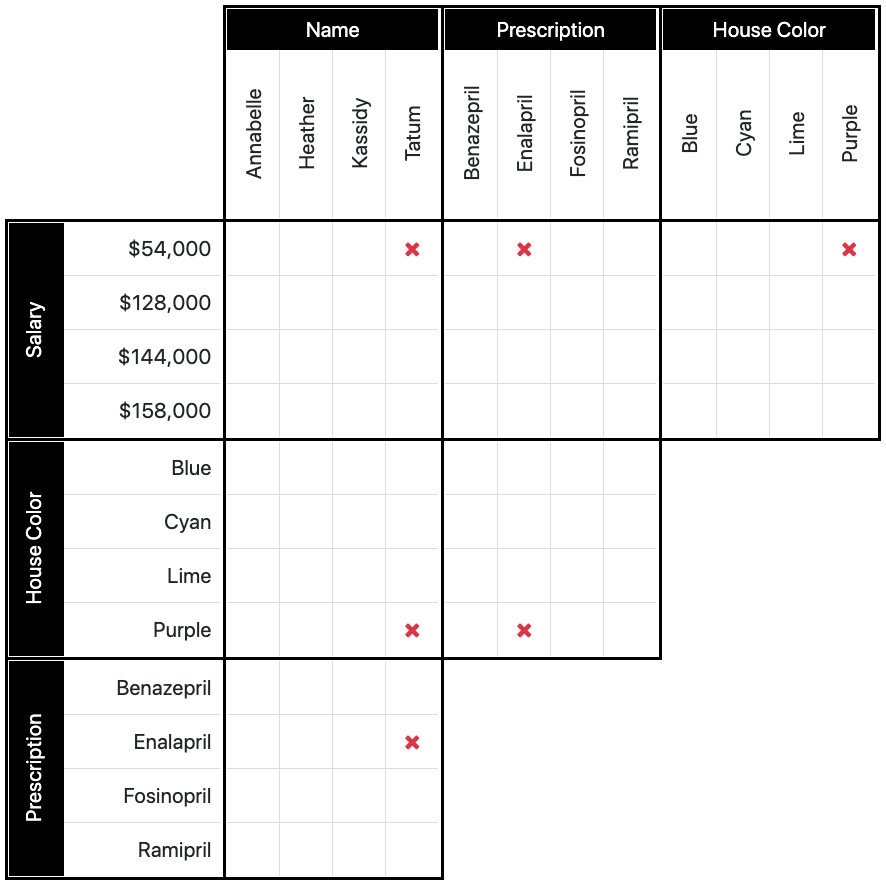
The 4 people were Tatum, the patient who was prescribed enalapril, the employee with the $54,000 salary, and the owner of the purple house.
The first 4 words of the clue tell us one thing: Each piece of information in this clue is a separate person. By that,
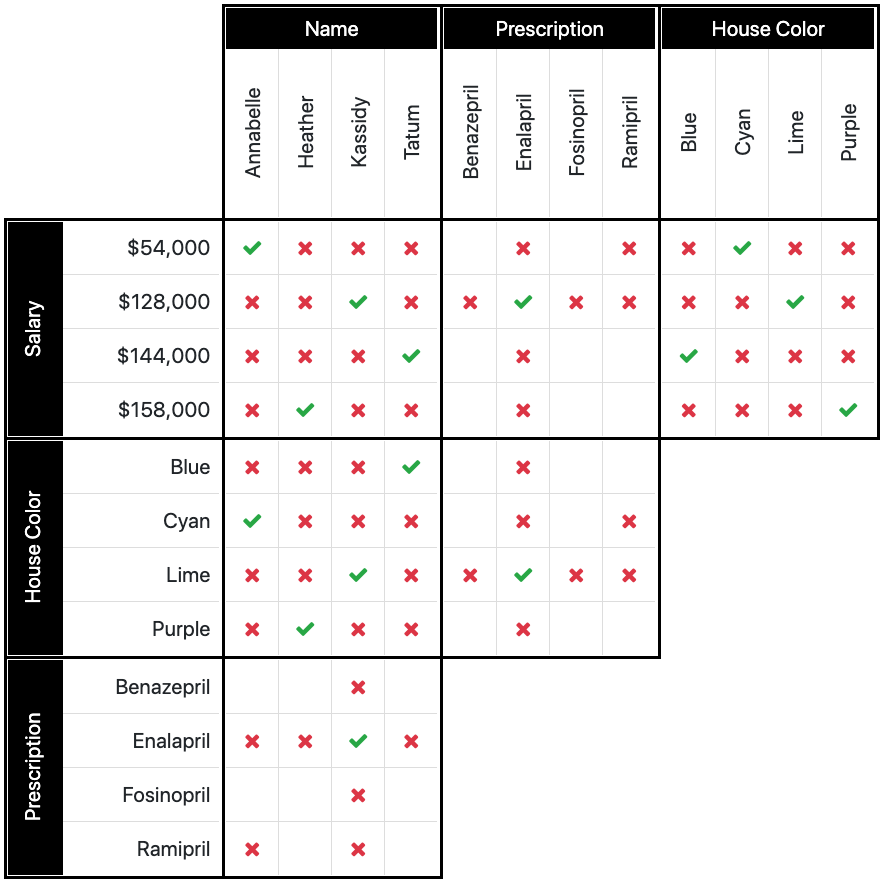
Starting in the top left box, we would find the row for $54,000. We find the box that represents Tatum and $54,000 and place an X inside that box as that combination cannot be true. Tatum does not earn $54,000. Moving across further, we find where $54,000 lines up with enalapril. As we know, again, that this combination cannot be true, we place an X there, as well. Finally, we place an X where $54,000 meets purple, as the person who earns $54,000 does not own the purple house.
We now move to the second row of boxes. We are concerned here with the purple house. We know that it does not belong to Tatum, so we can place an X where they meet, and likewise, an X where purple meets enalapril.
In the last box, we find enalapril. The only data we can compare with it in this box, are the persons names, and we know it is not Tatum in this case, so we place the final X. You can see the finished grid below.
Clue 2 says:
Of Tatum and Annabelle, one earns $144,000 per year and the other lives in the cyan colored house.
This clue is more complicated than the last clue. At first, you might assume that you can only rule out that the $144,000 salary is not the cyan colored house, because we have no way of knowing, at this point, which of the girls owns the cyan house, and which earns $144,000. But for now, go ahead and place your X in the $144,000/cyan combination in the 3rd box on the top row.
Now we can go a little further and rule out that for the $144,000, it can only be Tatum or Annabelle. Because of that, we can place an X in the $144,000/Heather combination, as well as in the $144,000/Kassidy combination, because from this clue we know that neither of those girls earns $144,000, again, it can only be Annabelle or Tatum. We can do the same in the next box down for the cyan house. Cyan/Heather and cyan/Kassidy cannot be true, so we place our X's.
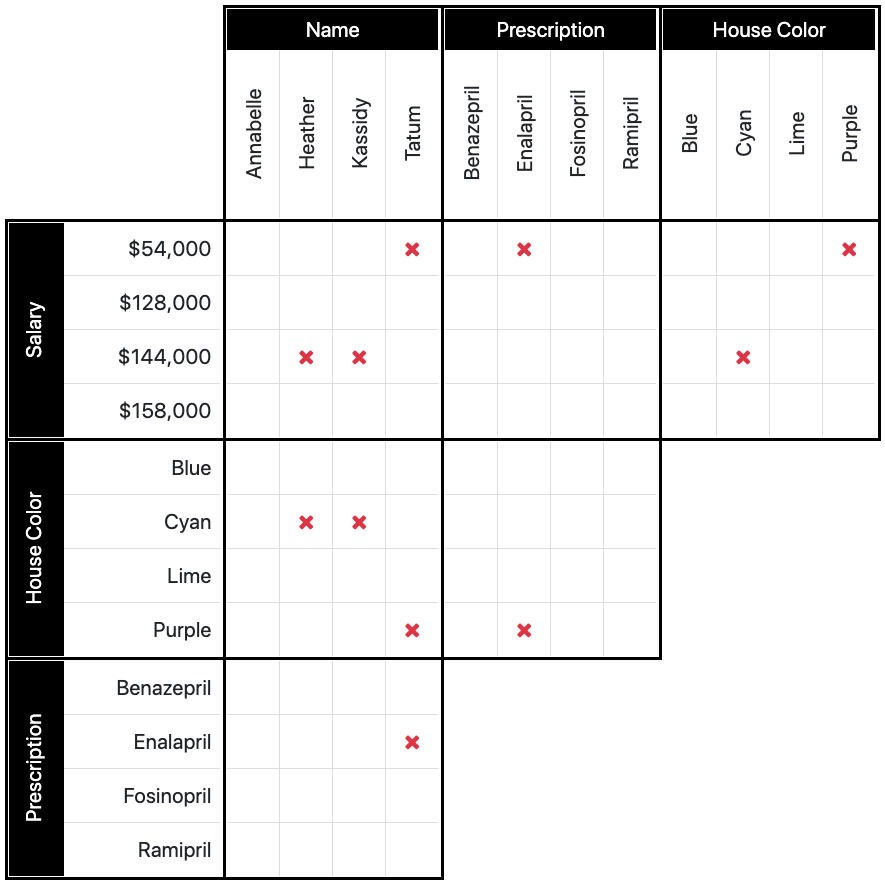
The patient who was prescribed enalapril is not Heather.
We place our X in the enalapril/Heather combination in the bottom box.
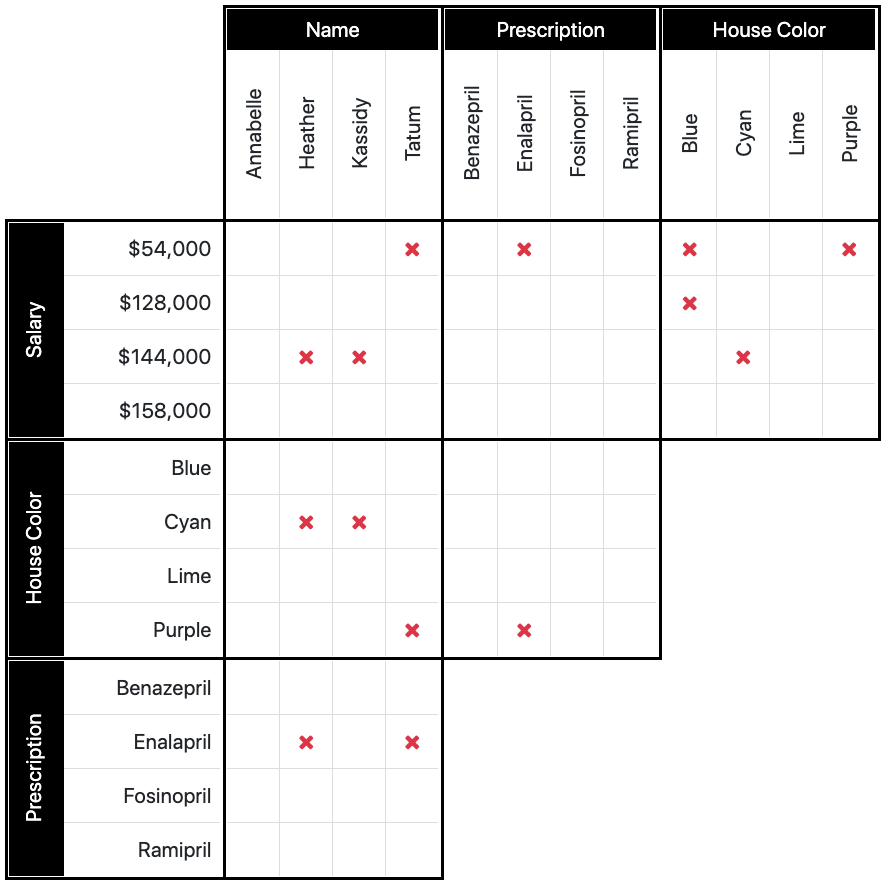
Either the employee with the $144,000 salary or the employee with the $158,000 salary lives in the blue colored house.
For clue 4, we can figure out that only one of those two salaries can be of the owner of the blue house. Therefore, we can place our X's in the $54,000/blue and the $128,000/blue combo's in the third box, top row.
We're going to look at the next three clues for this section.
Kassidy earns less than Heather.
By this clue, we can use logic to tell us that Kassidy cannot earn the most money, as she earns less than Heather. Likewise, Heather cannot earn the least amount, as she earns more than Kassidy. We can place our X's in Kassidy/$158,000 and in Heather/$54,000.
The owner of the blue house earns more than Kassidy.
This clue does not help us much at this point. We do not know how much the owner of the blue house earns, nor how much Kassidy earns. We have already determined earlier that the blue house does not earn the least money, so we do not need to place another X. For now, all we know is that Kassidy does not own the blue house. In the second row, first box, we can place an X in the blue/Kassidy combo. We might have to come back to this clue later.
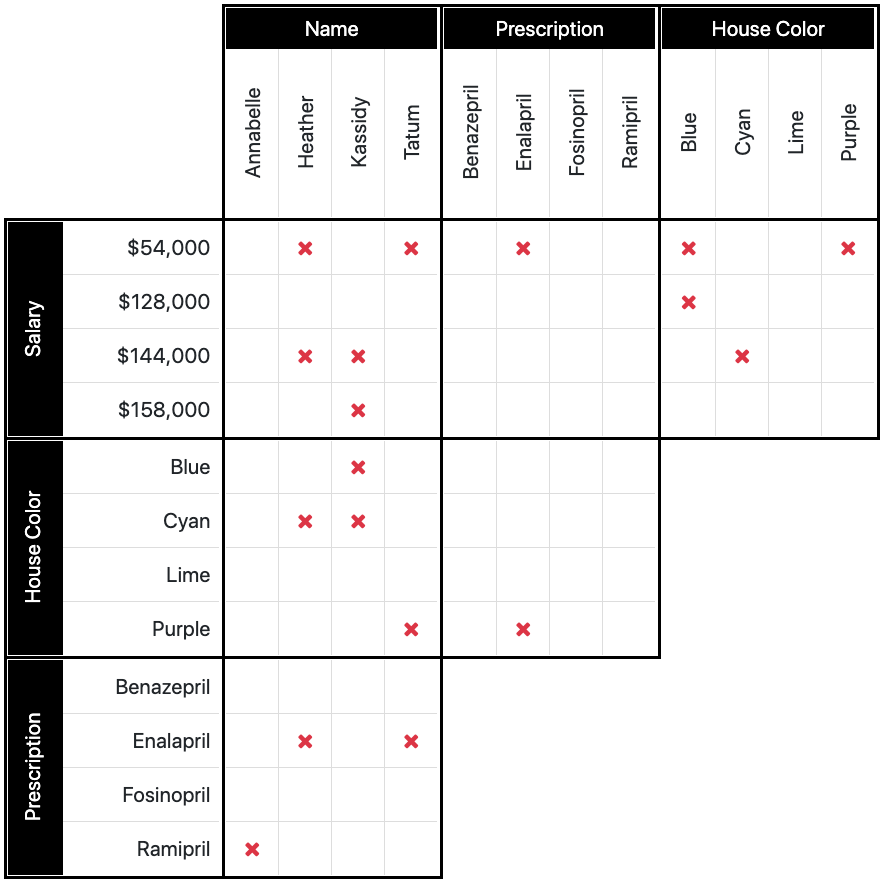
The patient who was prescribed ramipril is not Annabelle.
A simple statement. Bottom box, ramipril/Annabelle combo, place your X. Your grid should now look the same as ours.
The owner of the lime house was prescribed enalapril for their heart condition.
Now, things will start to get interesting. We finally have a statement that we know to be true. The lime colored house was prescribed enalapril. Because of this, we must do two things. We will first place an O where lime meets enalarpil in the second row, second box.
Because we know that that statement is true, we know that no other colored houses can be combined with enalapril, and we know that no other medications can be combined with the lime house. Therefore, we can X out the rest of the row and column where you placed your O. See the image 5a.
Image 5a
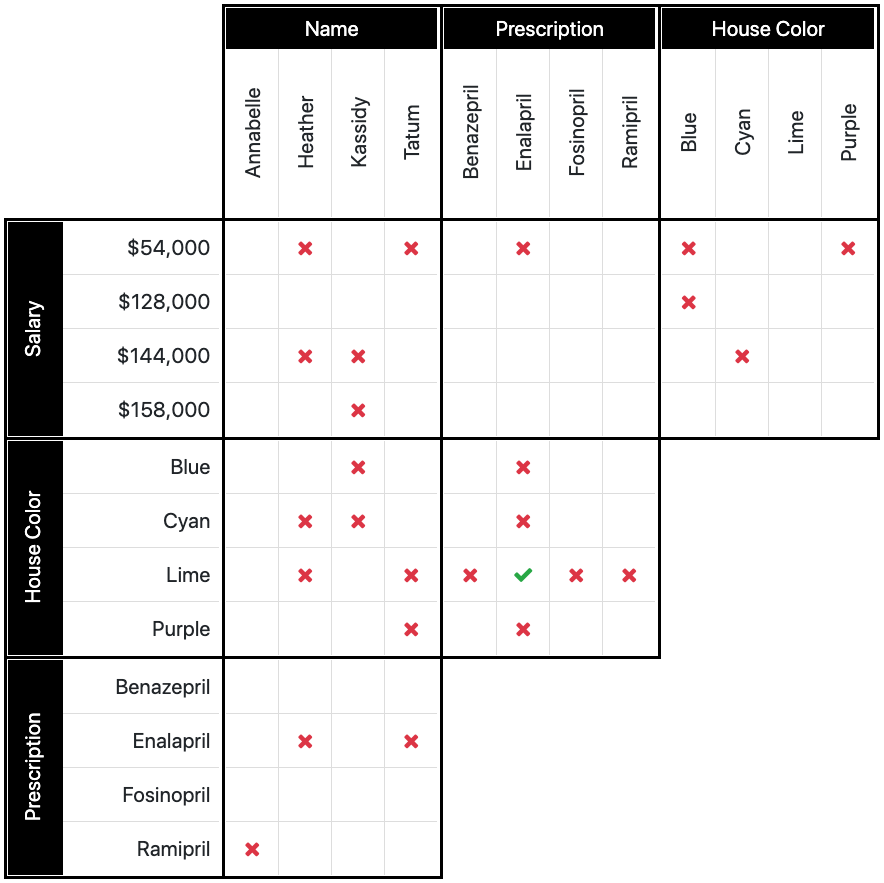
Image 5b
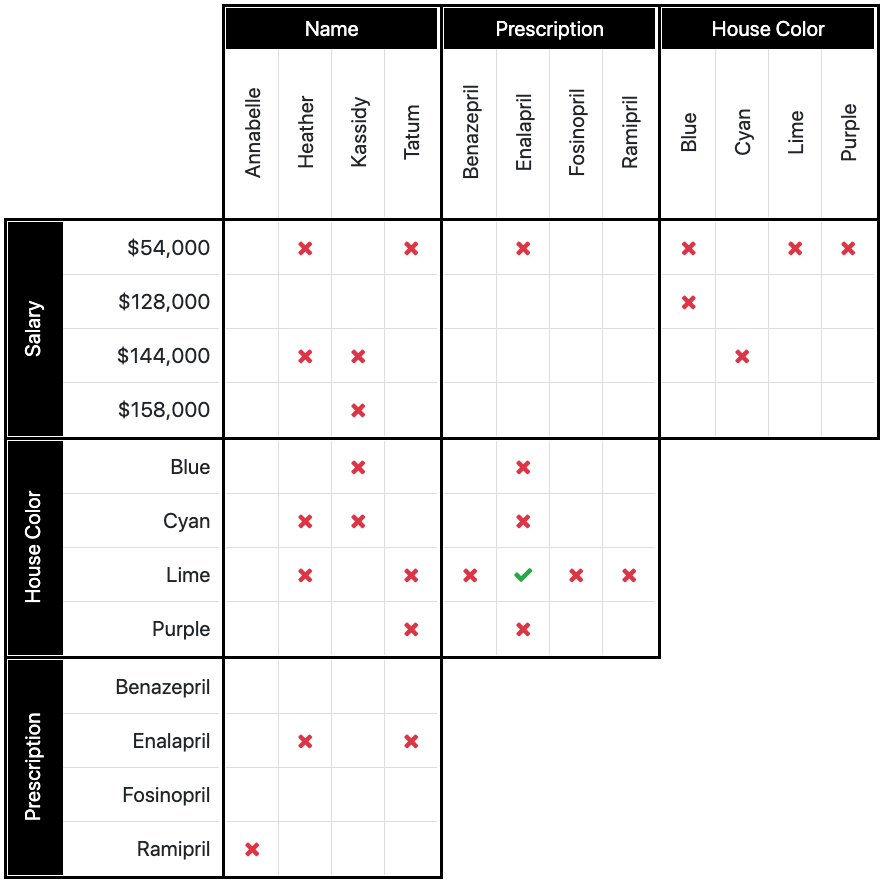
We have our first true combination! Now this is where the grid comes in handy the most. We need to look at the true statement, and find out if we can put any X's, or hopefully O's, into other boxes. Still looking at the top image (5a), find the O and look in the box above it' You will see an X in the $54,000/enalapril box. We know, therefore, that $54,000 is not enalapril, and so it cannot be lime. The logic is like this: if lime=enalapril and enalapril does not = $54,000, then $54,000 cannot = lime.
Because of that logic, we can now rule out the $54,000 income belonging to the lime colored house. So, we place our X in the 3rd box on the top row where $54,000/lime meet. See image 5b.
This leaves us in another interesting situation. Because 3 out of the 4 combinations have been found to be false ($54,000 is not blue, lime or purple), that only leaves one more combination. Because of that, it must be true. So now we can place an O for $54,000/cyan, and add X's to the rest of the column as they cannot be true. (cyan/128K, cyan/$144,000 which was already x'ed out, and cyan/$158,000.
Your box should now look like image 5c.
Image 5c
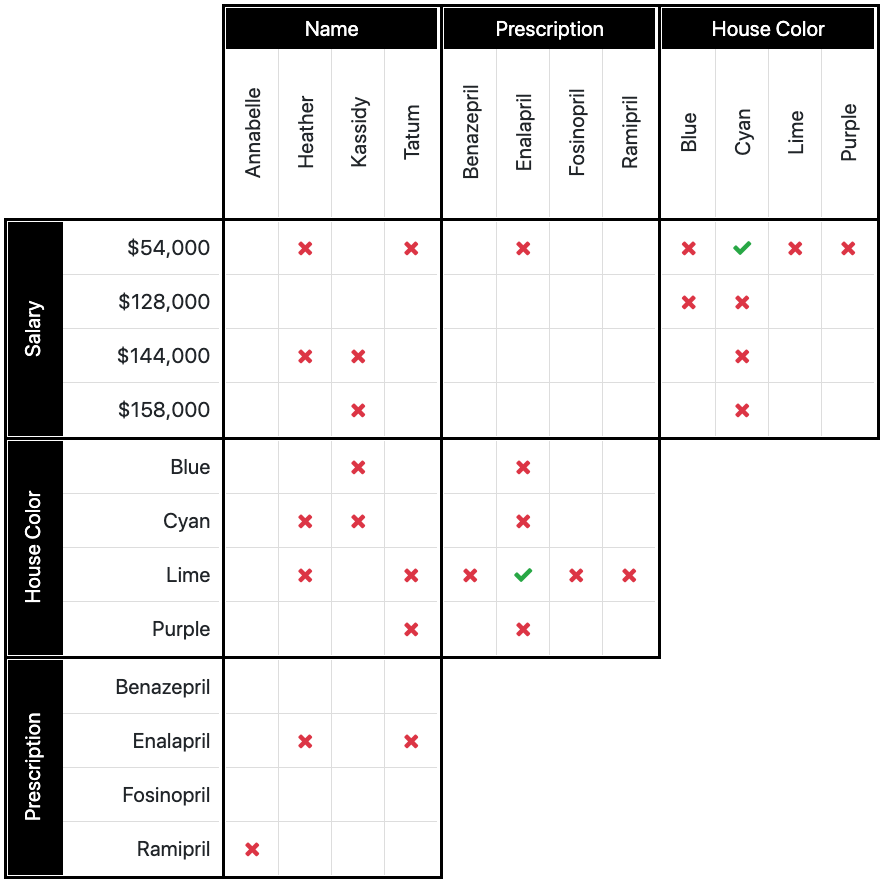
Image 5d
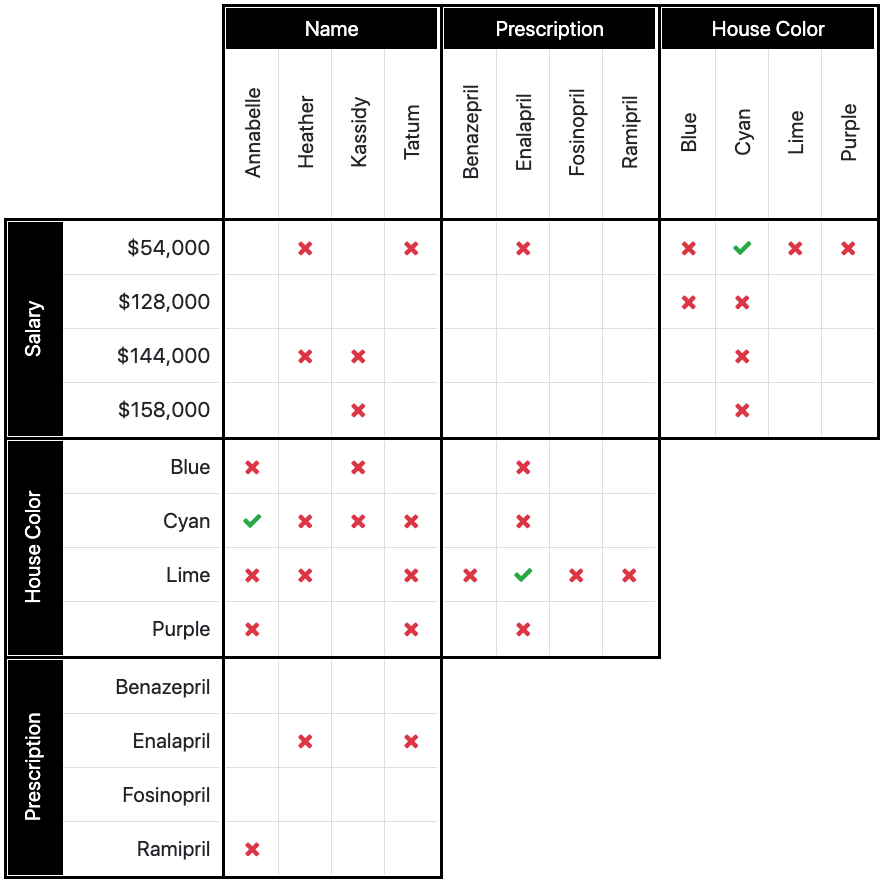
We will use the same procedure as above. Looking at the grid, you have a true condition where $54,000 and cyan meet. In the first box on the top row, we have determined earlier that Tatum does not earn $54,000, so we know because of that, she also does not live in the cyan house. (Again, if $54,000 = cyan, and Tatum does not = $54,000, then Tatum does not = cyan. Beautiful logic!)
Because of that, we can put an X in Tatum/cyan. Doing so leaves only one possible combination left for the cyan colored house, and that is cyan/Annabelle. So we also now know that Annabelle owns the cyan colored house. We will place an O there, for true. Image 5d.
We will quickly go through the rest of the moves available with this clue.
We have one last clue: The employee with the $144,000 salary was prescribed benazepril for their heart condition.
In the top row, 2nd box, we will set an O (true) for $144,000/benazepril. After placing our X's, we will see there is only one option left for ramipril, which is the $158,000 income. Set to true.
Fosinopril, which to this point was never mentioned, is the only choice left for $54,000 income. Set true.
At this point, all three boxes on the top row should be filled in completely! We now know all of the answers and do not need to work on the other boxes. (You can still fill them in, if you like.) Your grid should look like ours at this point.
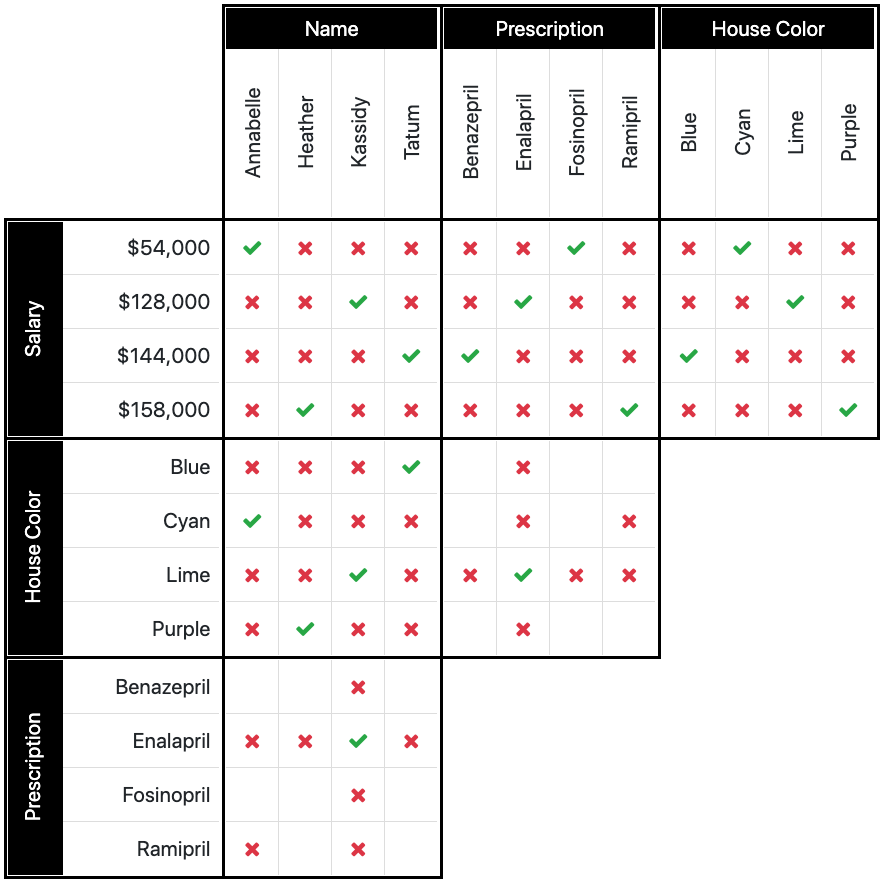
There is nothing left to do now, you have solved the puzzle! The answers are as follows:
| Salary | Name | Prescription | House Color |
|---|---|---|---|
| $54,000 | Annabelle | Fosinopril | Cyan |
| $128,000 | Kassidy | Enalapril | Lime |
| $144,000 | Tatum | Benazepril | Blue |
| $158,000 | Heather | Ramipril | Purple |
Congratulations! You've solved your first logic grid puzzle! Hopefully you weren't too confused by this tutorial! If you have any suggestions as to how we could make it better, please let us know.